こんばんは.
まるめがねです.
今回は強化学習についてまとめてみたいと思います.
強化学習と言えば, 囲碁のAlpha GOや電王戦に出てくるPonanzaなど人間の知能を超えたソフトウェアが開発されています.
もうプロ顔負けの能力を持った人工知能です.
これらの初期であるマルコフ決定過程についてまとめていきたいと思います.
はじめての勉強系記事の試み(笑)
強化学習とは
試行錯誤から環境に適応する学習制御の枠組みを強化学習と呼びます.
強化学習は, 一連の行動の良い・悪いを評価する「報酬:(スカラー)」という評価値を与え, これを手掛かりに学習を行っていきます.
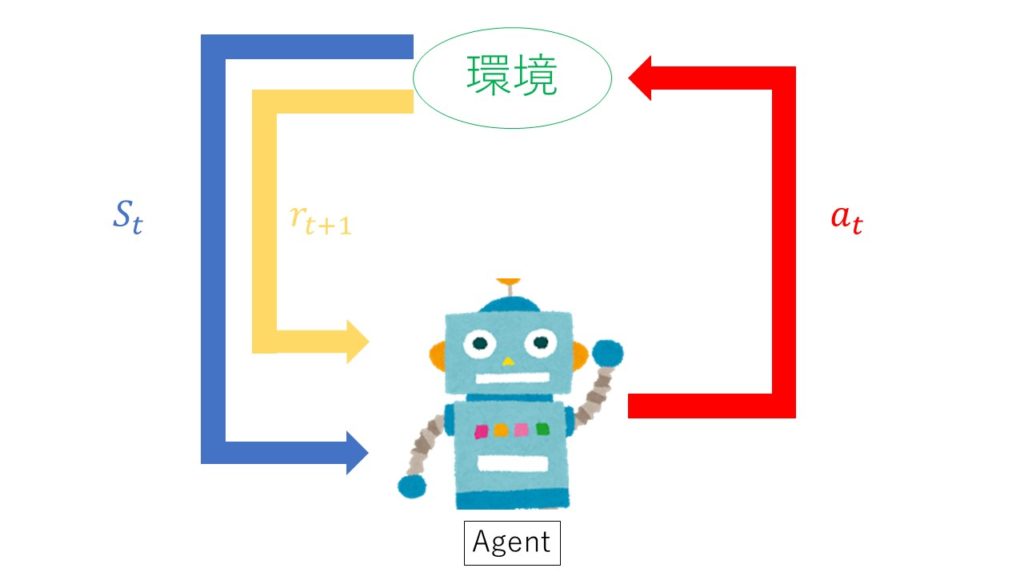
1. エージェントは時刻 t において環境の状態 s_t を観測
2. 観測した状態から行動a_tを決定
3. エージェントは行動を実行
4. 環境は新しい状態s_t+1に遷移
5. 遷移に応じた報酬r_t+1を獲得
6. 学習する
7. ステップ1から繰り返す
https://qiita.com/Hironsan/items/56f6c0b2f4cfd28dd906
強化学習の目的は, エージェントが取得する累積報酬を最大化するような, 状態から行動へのマッピング(政策)を獲得することです.
問題設定
MDPを説明するにあたって以下のような迷路を考えてみましょう.
迷路のルールは以下の通りです.
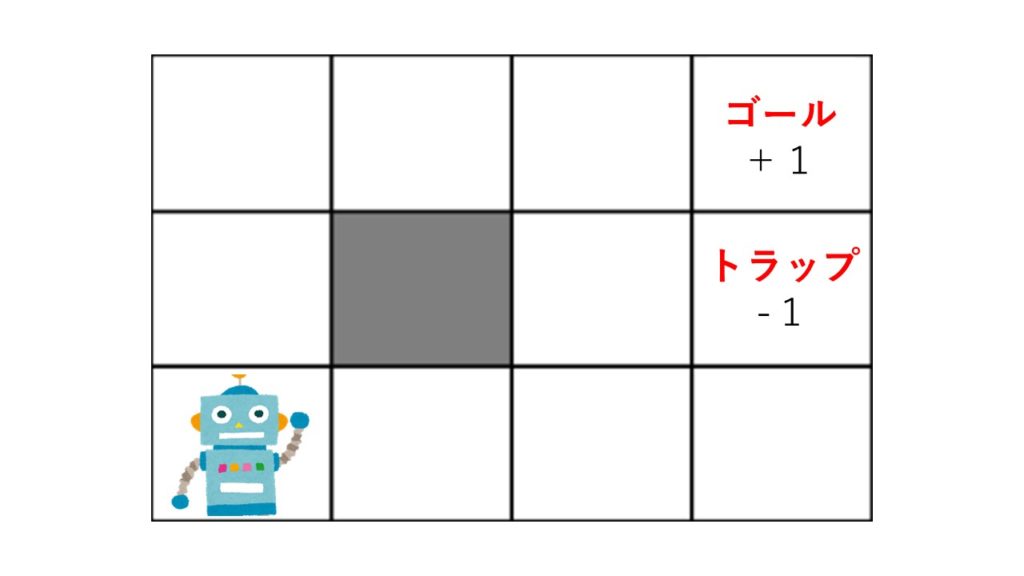
・エージェントはグリッドの中にいる.
・エージェントは壁(灰色)を越えられない.
・エージェントは自分が思った通りに動けるとは限らない. :80%の確率で正しく動けるが, 10%の確率で動こうと思った方向の左側に動き, もう10%の確率で右側へ動く.
・動こうと思った場所に壁があった場合は, その場にとどまる.
・エージェントは各時刻に報酬を受け取る.
・ゴールやトラップにたどり着くとゲームは終了し, スタート地点に戻る.
https://qiita.com/Hironsan/items/56f6c0b2f4cfd28dd906
確率的な遷移をもう少し詳しく説明します.
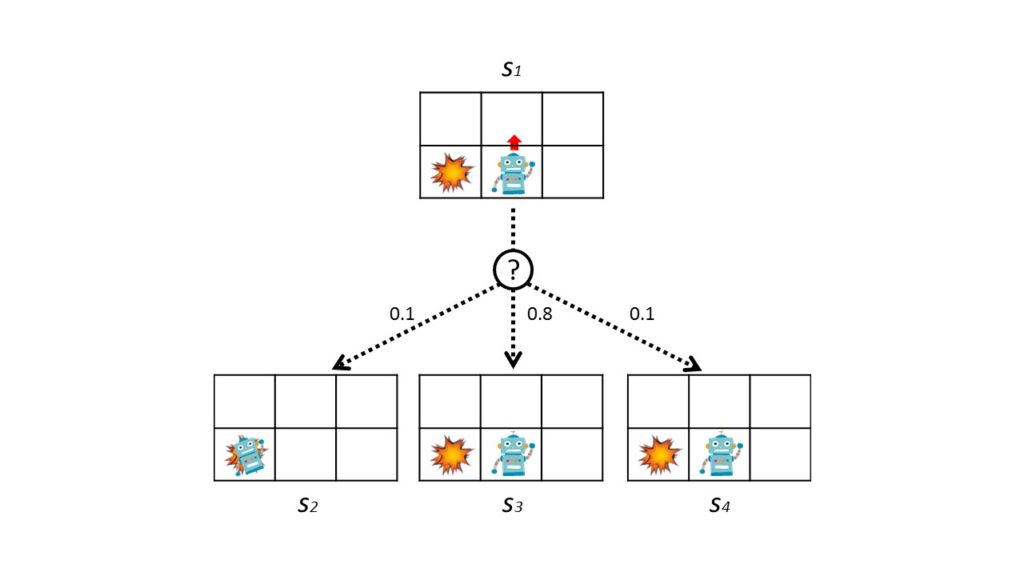
ロボットは上のように動こうとします.
このとき80%の確率で上に動きますが, 10%の確率で左側に動き, 残りの10%の確率で右側に動ききます.
遷移確率を表すと以下の表になります.
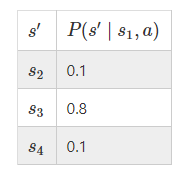
マルコフ決定過程 (Markov decision processes : MDP)
マルコフ決定過程(MDP)とは, 次に起こる事象の確率が, これまでの過程と関係なく, 現在の状態によってのみ決定される確率過程のことです.
このような, 以前の状態に依存しない性質のことを「マルコフ性」と言います.
さきほど設定した問題をMDPでモデル化します.
MDPは以下の4項の組で定義されます.
M = ( S, A, T, R)

状態集合:環境がとりうる状態の集合を表しています. 例題の場合は, グリッドすべてのセルを表しています.
行動集合:エージェントがとりうる行動の種類のことです. 例題の場合は, エージェントは上下左右に動くことができるので4種類です.
遷移確率:ある状態sで行動aをとった時に次の状態s‘へどのくらいの確率で遷移するかということを表しています.
報酬:観測した状態からとるべき行動を決定し, 新たに遷移した結果として環境から受け取る値のことです.
このMDPの目的は累積報酬を最大化する行動の戦略を学習することです. この行動の戦略のことを政策と呼びます.
MDPでは最適な政策π*:S → A を得ることが目的です. 政策は状態から行動へのマッピングを行う関数とみなせます.
報酬について
各時刻における報酬R(s_t)とすると, 累積報酬は以下の式になります.
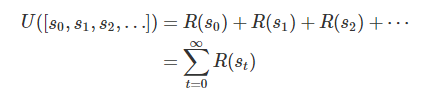
ただし, 将来の報酬をそのまま使うのはよくありません.
実際の環境では, 時間がたつと環境が変化するため, 時系列のすべての報酬を同じ重みで考慮するのは好ましくありません.
そのため, 将来得られる報酬より現在得られる報酬を重視するのです.

割引係数:γ(0<= γ < 1)
最適な政策の見つけ方
最適な政策を見つけるアルゴリズムとして, 今回は価値反復法を説明します.
価値反復法 (Value Iterarion)
価値反復法では, 状態s から最適な行動をとり続けた時の累積報酬を計算します.
この累積報酬が分かれば, 現在の状態s から将来にわたって得られる価値が分かるので, その価値を最大化するような行動を選択するようにするのです.
価値は以下の状態価値関数で求められます.
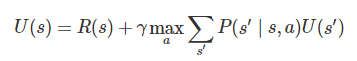

この式の中にはmaxという非線形計算があり行列等で解くことは困難です.
そのため反復的に計算を行って価値を徐々に更新していきます.
*P(s’|s, a)×U(s’)は期待値の計算
価値反復法のアルゴリズム
1.すべての状態s についてU(s) を適当な値(ゼロなど)に初期化
2.すべてのU(s)について以下の式を計算して値を更新
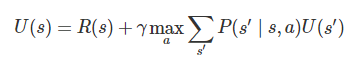
3. ステップ2を値が収束するまで繰り返す
おわりに
いかがだったでしょうか.
強化学習の初期であるマルコフ決定過程をまとめてみました.
いい勉強になりましたかね.
それでは!!




コメント